2020年湖南成人高考專升本《數(shù)學(xué)(一)》考試大綱

　　高等數(shù)學(xué)(一)

　　本大綱適用于工學(xué)、理學(xué)(生物科學(xué)類、地理科學(xué)類、環(huán)境科學(xué)類、心理學(xué)類等四個一級學(xué)科除外)專業(yè)的考生.

　　總 要 求

　　考生應(yīng)按本大綱的要求,了解或理解"高等數(shù)學(xué)"中極限和連續(xù)、一元函數(shù)微分學(xué)、一元函數(shù)積分學(xué)、空間解析幾何、多元函數(shù)微積分學(xué)、無窮級數(shù)、常微分方程的基本概念與基本理論;學(xué)會、掌握或熟練掌握上述各部分的基本方法.應(yīng)注意各部分知識的結(jié)構(gòu)及知識的內(nèi)在聯(lián)系;應(yīng)具有一定的抽象思維能力、邏輯推理能力、運(yùn)算能力、空間想象能力;能運(yùn)用基本概念、基本理論和基本方法正確地推理證明,準(zhǔn)確地計算;能綜合運(yùn)用所學(xué)知識分析并解決簡單的實際問題.

　　本大綱對內(nèi)容的要求由低到高,對概念和理論分為"了解"和"理解"兩個層次;對方法和運(yùn)算分為"會"、"掌握"和"熟練掌握"三個層次.

　　復(fù)習(xí)考試內(nèi)容

　　一、極限和連續(xù)

　　(一)極限

　　1.知識范圍

　　(1)數(shù)列極限的概念與性質(zhì)數(shù)列極限的定義

　　唯一性 有界性 四則運(yùn)算法則 夾逼定理 單調(diào)有界數(shù)列極限存在定理

　　(2)函數(shù)極限的概念與性質(zhì)

　　函數(shù)在一點處極限的定義 左、右極限及其與極限的關(guān)系 x趨于無窮(x→oo,I→+co,x→-co)時函數(shù)的極限 唯一性 四則運(yùn)算法則 夾逼定理

　　(3)無窮小量與無窮大量

　　無窮小量與無窮大量的定義 無窮小量與無窮大量的關(guān)系 無窮小量的性質(zhì) 無窮小量的比較

　　(4)兩個重要極限

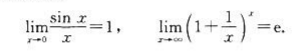
　　2.要求

　　(1)理解極限的概念(對極限定義中"e-N"、"e-8"、"e-M"等形式的描述不作要求).會求函數(shù)在一點處的左極限與右極限,了解函數(shù)在一點處極限存在的充分必要條件.

　　(2)了解極限的有關(guān)性質(zhì),掌握極限的四則運(yùn)算法則.

　　(3)理解無窮小量、無窮大量的概念,掌握無窮小量的性質(zhì)、無窮小量與無窮大量的關(guān)系.會進(jìn)行無窮小量的比較(高階、低階、同階和等價).會運(yùn)用等價r無窮小量代換求極限.

　　(4)熟練掌握用兩個重要極限求極限的方法.

　　(二)連續(xù)

　　1.知識范圍

　　(1)函數(shù)連續(xù)的概念

　　函數(shù)在一點處連續(xù)的定義 左連續(xù)與右連續(xù) 函數(shù)在一點處連續(xù)的充分必要條件 函數(shù)的間斷點

　　(2)函數(shù)在一點處連續(xù)的性質(zhì)

　　連續(xù)函數(shù)的四則運(yùn)算 復(fù)合函數(shù)的連續(xù)性 反函數(shù)的連續(xù)性

　　(3)閉區(qū)間上連續(xù)函數(shù)的性質(zhì)

　　有界性定理 最大值與最小值定理 介值定理(包括零點定理)

　　(4)初等函數(shù)的連續(xù)性

　　(1)理解函數(shù)在一點處連續(xù)與間斷的概念,理解函數(shù)在一點處連續(xù)與極限存在的關(guān)系,掌握函數(shù)(含分段函數(shù))在一點處的連續(xù)性的判斷方法.

　　(2)會求函數(shù)的間斷點.

　　(3)掌握在閉區(qū)間上連續(xù)函數(shù)的性質(zhì),會用介值定理推證一些簡單命題.

　　(4)理解初等函數(shù)在其定義區(qū)間上的連續(xù)性,會利用連續(xù)性求極限.

　　二、一元函數(shù)微分學(xué)

　　(一)導(dǎo)數(shù)與微分

　　1.知識范圍

　　(1)導(dǎo)數(shù)概念

　　導(dǎo)數(shù)的定義 左導(dǎo)數(shù)與右導(dǎo)數(shù) 函數(shù)在一點處可導(dǎo)的充分必要條件 導(dǎo)數(shù)的幾何意義與物理意義 可導(dǎo)與連續(xù)的關(guān)系

　　(2)求導(dǎo)法則與導(dǎo)數(shù)的基本公式

　　導(dǎo)數(shù)的四則運(yùn)算 反函數(shù)的導(dǎo)數(shù) 導(dǎo)數(shù)的基本公式

　　(3)求導(dǎo)方法

　　復(fù)合函數(shù)的求導(dǎo)法 隱函數(shù)的求導(dǎo)法 對數(shù)求導(dǎo)法 由參數(shù)方程確定的函數(shù)的求導(dǎo)法 求分段函數(shù)的導(dǎo)數(shù)

　　(4)高階導(dǎo)數(shù)

　　高階導(dǎo)數(shù)的定義 高階導(dǎo)數(shù)的計算

　　(5)微分

　　微分的定義 微分與導(dǎo)數(shù)的關(guān)系 微分法則一階微分形式不變性

　　2. 要求

　　(1)理解導(dǎo)數(shù)的概念及其幾何意義,了解可導(dǎo)性與連續(xù)性的關(guān)系, 掌握用定義求函數(shù)在一點處的導(dǎo)數(shù)的方法.

　　(2)會求曲線上一點處的切線方程與法線方程.

　　(3)熟練掌握導(dǎo)數(shù)的基本公式、四則運(yùn)算法則及復(fù)合函數(shù)的求導(dǎo)

　　方法,會求反函數(shù)的導(dǎo)數(shù).

　　(4)掌握隱函數(shù)求導(dǎo)法、對數(shù)求導(dǎo)法以及由參數(shù)方程所確定的函數(shù)的求導(dǎo)方法,會求分段函數(shù)的導(dǎo)數(shù).

　　(5)理解高階導(dǎo)數(shù)的概念,會求簡單函數(shù)的 n階導(dǎo)數(shù).

　　(6)理解函數(shù)的微分概念,掌握微分法則,了解可微與可導(dǎo)的關(guān)系,會求函數(shù)的一階微分.

　　(二)微分中值定理及導(dǎo)數(shù)的應(yīng)用

　　1.知識范圍

　　(1)微分中值定理

　　羅爾(Rolle)定理 拉格朗日(Lagrange)中值定理

　　(2)洛必達(dá)(I.'Hospital)法則

　　(3)函數(shù)單調(diào)性的判定法

　　(4)函數(shù)的極值與極值點、最大值與最小值

　　(5)曲線的凹凸性、拐點

　　(6)曲線的水平漸近線與鉛直漸近線

　　2.要求

　　(1)理解羅爾定理、拉格朗日中值定理及它們的幾何意義.會用拉格朗日中值定理證明簡單的不等式.

　　)熟練掌握用洛必達(dá)法則求

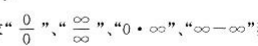
　　型

　　未定式的極限的方法.

　　(3)掌握利用導(dǎo)數(shù)判定函數(shù)的單調(diào)性及求函數(shù)的單調(diào)增、減區(qū)間的方法,會利用函數(shù)的單調(diào)性證明簡單的不等式.

　　(4)理解函數(shù)極值的概念.掌握求函數(shù)的駐點、極值點、極值、最大值與最小值的方法,會解簡單的應(yīng)用問題.

　　(5)會判斷曲線的凹凸性,會求曲線的拐點.

　　(6)會求曲線的水平漸近線與鉛直漸近線.

　　三、一元函數(shù)積分學(xué)

　　(一)不定積分

　　1.知識范圍

　　(1)不定積分

　　原函數(shù)與不定積分的定義 原函數(shù)存在定理 不定積分的性質(zhì)(2)基本積分公式

　　(3)換元積分法

　　第一換元法(湊微分法)第二換元法

　　(4)分部積分法

　　(5)一些簡單有理函數(shù)的積分

　　2.要求

　　(1)理解原函數(shù)與不定積分的概念及其關(guān)系,掌握不定積分的性質(zhì),了解原函數(shù)存在定理.

　　(2)熟練掌握不定積分的基本公式.

　　(3)熟練掌握不定積分第一換元法,掌握第二換元法(限于三角代換與簡單的根式代換).

　　(4)熟練掌握不定積分的分部積分法.

　　(5)會求簡單有理函數(shù)的不定積分.

　　(二)定積分

　　1.知識范圍

　　(1)定積分的概念

　　定積分的定義及其幾何意義 可積條件

　　(2)定積分的性質(zhì)

　　(3)定積分的計算

　　變上限積分 牛頓-萊布尼茨(Newton-Leibniz)公式 換元積分法分部積分法

　　(4)無窮區(qū)間的反常積分

　　(5)定積分的應(yīng)用

　　平面圖形的面積 旋轉(zhuǎn)體的體積

　　2.要求

　　(1)理解定積分的概念及其幾何意義,了解函數(shù)可積的條件.

　　(2)掌握定積分的基本性質(zhì).

　　(3)理解變上限積分是變上限的函數(shù),掌握對變上限積分求導(dǎo)數(shù)的方法.

　　(4)熟練掌握牛頓-萊布尼茨公式.

　　(5)掌握定積分的換元積分法與分部積分法.

　　(6)理解無窮區(qū)間的反常積分的概念,掌握其計算方法.

　　(7)掌握直角坐標(biāo)系下用定積分計算平面圖形的面積以及平面圖形繞坐標(biāo)軸旋轉(zhuǎn)所生成的旋轉(zhuǎn)體的體積.

　　四、空間解析幾何

　　(一)平面與直線

　　1.知識范圍

　　(1)常見的平面方程

　　點法式方程 一般式方程

　　(2)兩平面的位置關(guān)系(平行、垂直)

　　(3)空間直線方程

　　標(biāo)準(zhǔn)式方程(又稱對稱式方程或點向式方程)一般式方程

　　(4)兩直線的位置關(guān)系(平行、垂直)

　　(5)直線與平面的位置關(guān)系(平行、垂直和直線在平面上)

　　2.要求

　　(1)會求平面的點法式方程、一般式方程.會判定兩平面的垂直、平行.

　　(2)了解直線的一般式方程,會求直線的標(biāo)準(zhǔn)式方程.會判定兩直線平行、垂直.

　　(3)會判定直線與平面間的關(guān)系(垂直、平行、直線在平面上).

　　(二)簡單的二次曲面

　　1.知識范圍

　　球面 母線平行于坐標(biāo)軸的柱面 旋轉(zhuǎn)拋物面 圓錐面 橢球面

　　2.要求

　　了解球面、母線平行于坐標(biāo)軸的柱面、旋轉(zhuǎn)拋物面、圓錐面和橢球面的方程及其圖形.

　　五、多元函數(shù)微積分學(xué)

　　(一)多元函數(shù)微分學(xué)

　　1. 知識范圍

　　(1)多元函數(shù)

　　多元函數(shù)的定義 二元函數(shù)的幾何意義 二元函數(shù)極限與連續(xù)的概念

　　(2)偏導(dǎo)數(shù)與全微分

　　偏導(dǎo)數(shù) 全微分二階偏導(dǎo)數(shù)

　　(3)復(fù)合函數(shù)的偏導(dǎo)數(shù)

　　(4)隱函數(shù)的偏導(dǎo)數(shù)

　　(5)二元函數(shù)的無條件極值與條件極值

　　2.要求

　　(1)了解多元函數(shù)的概念、二元函數(shù)的幾何意義.會求二元函數(shù)的表達(dá)式及定義域.了解二元函數(shù)的極限與連續(xù)概念(對計算不作要求),

　　(2)理解偏導(dǎo)數(shù)概念,了解偏導(dǎo)數(shù)的幾何意義,了解全微分概念, 了解全微分存在的必要條件與充分條件.

　　(3)掌握二元函數(shù)的一、二階偏導(dǎo)數(shù)計算方法.

　　(4)掌握復(fù)合函數(shù)一階偏導(dǎo)數(shù)的求法.

　　(5)會求二元函數(shù)的全微分.

　　(6)掌握由方程F(x,y,z)=0所確定的隱函數(shù)z=z(x,y)的一階偏導(dǎo)數(shù)的計算方法.

　　(7)會求二元函數(shù)的無條件極值.會用拉格朗日乘數(shù)法求二元函數(shù)的條件極值.

　　(二)二重積分

　　1.知識范圍

　　(1)二重積分的概念

　　二重積分的定義 二重積分的幾何意義

　　(2)二重積分的性質(zhì)

　　(3)二重積分的計算

　　(4)二重積分的應(yīng)用

　　2.要求

　　(1)理解二重積分的概念及其性質(zhì).

　　(2)掌握二重積分在直角坐標(biāo)系及極坐標(biāo)系下的計算方法.

　　(3)會用二重積分解決簡單的應(yīng)用問題(限于空間封閉曲面所圍成的有界區(qū)域的體積、平面薄板的質(zhì)量).

　　六、無窮級數(shù)

　　(一)數(shù)項級數(shù)

　　1. 知識范圍

　　(1)數(shù)項級數(shù)

　　數(shù)項級數(shù)的概念 級數(shù)的收斂與發(fā)散 級數(shù)的基本性質(zhì) 級數(shù)收斂的必要條件

　　(2)正項級數(shù)收斂性的判別法

　　比較判別法 比值判別法

　　(3)任意項級數(shù)

　　交錯級數(shù) 絕對收斂 條件收斂 菜布尼茨判別法

　　2.要求

　　(1)理解級數(shù)收斂、發(fā)散的概念.掌握級數(shù)收斂的必要條件,了解級數(shù)的基本性質(zhì).

　　(2)會用正項級數(shù)的比值判別法與比較判別法.

　　斂性.

　　(4)了解級數(shù)絕對收斂與條件收斂的概念,會使用萊布尼茨判別法.

　　(二)冪級數(shù).關(guān)注公眾號

　　1.知識范圍點擊圖田,關(guān)注公眾號

　　免費(fèi)領(lǐng)取底考謂程。材相

　　(1)冪級數(shù)的概念

　　收斂半徑 收斂區(qū)間

　　(2)冪級數(shù)的基本性質(zhì)

　　(3)將簡單的初等函數(shù)展開為冪級數(shù)

　　2.要求

　　(1)了解冪級數(shù)的概念.

　　(2)了解冪級數(shù)在其收斂區(qū)間內(nèi)的基本性質(zhì)(和、差、逐項求導(dǎo)與逐項積分).

　　(3)掌握求冪級數(shù)的收斂半徑、收斂區(qū)間(不要求討論端點)的方法.

　　的麥克勞林(Ma-

　　claurin)公式,將一些簡單的初等函數(shù)展開為x或x一x。的冪級數(shù).

　　七、常微分方程

　　(一)一階 微分方程

　　1.知識范圍

　　(1)微分方程的概念

　　微分方程的定義 階 解 通解 初始條件 特解

　　(2)可分離變量的方程

　　(3)一階線性方程

　　2.要求

　　(1)理解微分方程的定義,理解微分方程的階、解、通解、初始條件和特解.

　　(2)掌握可分離變量方程的解法.

　　(3)掌握一階線性方程的解法.

　　(二)二階線性微分方程

　　1.知識范圍

　　(1)二階線性微分方程解的結(jié)構(gòu)

　　(2)二階常系數(shù)齊次線性微分方程

　　(3)二階常系數(shù)非齊次線性微分方程

　　2.要求

　　(1)了解二階線性微分方程解的結(jié)構(gòu).

　　(2)掌握二階常系數(shù)齊次線性微分方程的解法.

　　(3)掌握二階常系數(shù)非齊次線性微分方程的解法(自由項限定為f(x)=P,(x)e",其中P。(x)為x的n次多項式,a為實常數(shù)).

　　考試形式及試卷結(jié)構(gòu)

　　試卷總分:150分

　　考試時間:150分鐘

　　考試方式:閉卷,筆試

　　試卷內(nèi) 容比例:

　　極限和連續(xù)約13%

　　一元函數(shù)微分學(xué)

　　約25%

　　約25%

　　一元函數(shù)積分學(xué)

　　多元函數(shù)微積分(含空間解析幾何)

　　約20%

　　無窮級數(shù)約7%

　　常微分方程約10%

　　試卷題型比例:

　　約27%選擇題

　　填空題

　　約27%

　　約46%解答題

　　試題難易比例:

　　約30%容易題

　　約50%

　　中等難度題約20%

　　較難題約20%

　　想獲取更多關(guān)于未知的相關(guān)資訊，如成人高考報名時間、報考條件、考試時間、備考知識、錄取查詢、相關(guān)新聞等，敬請關(guān)注湖南成人高考網(wǎng)(m.strawberry17.com)或關(guān)注官方微信公眾號“湖南成考中心”???????如有更多疑問也可以直接聯(lián)系我們招生老師，聯(lián)系電話：0731-89903663。